Why do we need it?
We need the Law of Sines when we are not sure if a triangle is a right triangle.
How is it derived from what we already know?
Since we don't know if the triangle we're given is a right triangle, we can't use the trig ratios we used in the Unit Circle. However, we can use trig functions. Say we're given the triangle below.
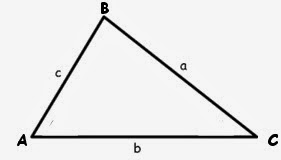
We don't know if it is a right triangle, but that doesn't matter because we can just do this
If you remember geometry trig, you'll remember a handy mnemonic: SOH CAH TOA. SOH means "sine equals opposite over hypotenuse", and in this case, the opposite side from angle A is the green line h while the hypotenuse is side C. Therefore, we can say that sineA= h/c.
But what about the other triangle we made? We can apply SOH to this triangle too, and we get sinC=h/a.
As you can see, h is in both of these equations, so if we fiddle a bit to get h by itself in both equations (multiplying both sides by c in the first, multiplying both sides by a in the second), we can set the two equal to each other. Now we have c(sinA)= a(sinC). Fiddle around a bit more (and by that I mean divide both sides by ac- a term both sides have) and you're left with the Law of Sines...sort of.

It's almost there, but what about angle B? We can't just leave it all by itself!
Not to worry, we can just make another green perpendicular line and do the same thing, only with different angles.
In this case, SOH for the two triangles are sinA=h/b and sinB=h/a. Do the same fiddling to get h by itself to set the two equations equal to each other and we get b(sinA)=a(sinB). Fiddle again and we end with this lovely bit:
Still not the Law of Sines, but we're close. As you can see, both equations have sinA/a in them. Which means...we can set them equal to each other! Yay! And for added fun, we don't even have to get rid of sinA/a! We can just mash them together to get this:

And there's the Law of Sines. Isn't it lovely?
[4] Area Formulas
How is the “area of an oblique” triangle derived? How does it relate to the area formula that you are familiar with?I'm going to go ahead and answer both of these questions in one chunk. Less reading, how lucky for you!
Below are some examples of an oblique triangle (aka a triangle with all sides not being equal.)

As you can see, we start by doing the same thing we did before- make right triangles with a perpendicular line called h because mathematicians love right triangles more and we already know how to work with them.
If you recall from reading the Law of Sines section above, you'll know that we can get h by itself at some point with any of the angles. you have the option of a(sinB), a(sinC), b(sinA), b(sinC), c(sinA) and c(sinB) depending on which angle you sacrificed to draw h. Why is getting h by itself so important, you might ask? Again, if you remember geometry, you'll know the area of a triangle is usually given as a=1/2(b)(h). Oh look at that, there's an h in that equation that we can conveniently substitute any of the above options into, how fortunate for us!
Let's go with the first option, a(sinC) for simplicity's sake. When we substitute that value into the area equation, we get...
/drumrolls/
...1/2 (b)(a)(sinC)! And that's our area of an oblique triangle equation.
References:
http://www.mathsisfun.com/algebra/trig-sine-law.html
http://www.regentsprep.org/Regents/math/algtrig/ATT12/lawofsines.htm
http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm



No comments:
Post a Comment