Wednesday, March 26, 2014
SP#7: Unit Q Concept 2: Pythagorean/Ratio/Reciprocal Identities with SOH CAH TOA
This SP was made in collaboration with Leslie N. and can be seen by clicking this word right here. While you're there, be sure to check out her awesome math posts too!
Wednesday, March 19, 2014
ID# 3: Unit Q Concept 1: Pythagorean Identities
Inquiry Activity Summary
1.) Where does where sin2x+cos2x=1 come from to begin with (think Unit Circle!).
Well to answer this question we first have to think about the Pythagorean Theorem. It's an identity (which means it's a proven formula hat's always true) and we used it a lot when dealing with the Unit Circle. The variables we used were x (later we'll use x in the final form but in that case x stands for the angle), y, and r; so the formula was x^2 + y^2 = r^2. (I'll explain why the Unit Circle is important in a bit.)
Let's say we wanted the equation to equal 1. The easiest way to make that happen is to divide everything by r^2, which would leave us with x^2/r^2 + y^2/r^2 = 1.
Coincidentally, the cosine and sine ratios for the Unit Circle are x/r and y/r. Huh. Scratch that, not so coincidental.
If we replaced the ratios with sine and cosine (and switched the positions of sine and cosine but that's okay because it's addition), we'd get sin^2x + cos^2x = 1, which is the Pythagorean Identity!
2.) Show and explain how to derive the two remaining Pythagorean Identities from sin2x+cos2x=1. Be sure to show step by step.
The remaining two Pythagorean Identities are 1 + tan^2x = sec^2x and 1 + cot^2x = csc^2x.
We'll start with the Pythagorean Theorem again: x^2 + y^2 = r^2. Instead of dividing by r^2, let's divide by x^2 and make the x term equal to 1. When we do that, we end up with 1 + y^2/x^2 = r^2/x^2. In the Unit Circle, y/x is the ratio for tangent and r/x is the ratio for secant. Replace them and you end up with 1 + tan^2x = sec^2x- another Pythagorean Identity!
Two down, we've got one to go. Start with the Pythagorean Theorem again: x^2 + y^2 = r^2. We've already used r^2 and x^2, so let's go with our last variable squared y^2. When you divide everything by y^2, you get x^2/y^2 + 1 = r^2/y^2. In the Unit Circle, x/y is the ratio for cotangent and r/y is the ratio for cosecant. Replace them (and switch the x and y terms around if you like) and you end up with 1 + cot^2x = csc^2x- the last Pythagorean Identity.
Inquiry Activity Reflection
1.) “The connections that I see between Units N, O, P, and Q so far are…”
The connections I see between the three units are the use of the Unit Circle and the use of trigonometric ratios.
“If I had to describe trigonometry in THREE words, they would be…”
The three words would be "memorization", "ratios", and "angles".
Monday, March 17, 2014
WPP#13 &14: Unit P Concepts 6 & 7: Laws of Sine and Cosine
This WPP was a collaboration between myself and Leslie N. Go here to check out more of her cute math posts! If you'd rather stay here, luckily for you there's a lovely WPP right below for you to check out her math anyway~
Create your own Playlist on LessonPaths!
Sunday, March 16, 2014
BQ# 1: Unit P: Concepts 1 and 4
[1] Law of Sines
Why do we need it?
We need the Law of Sines when we are not sure if a triangle is a right triangle.
How is it derived from what we already know?
Since we don't know if the triangle we're given is a right triangle, we can't use the trig ratios we used in the Unit Circle. However, we can use trig functions. Say we're given the triangle below.
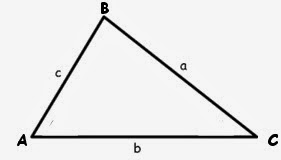
We don't know if it is a right triangle, but that doesn't matter because we can just do this
and bam! We've got two right triangles! We can call the green perpendicular line h.
If you remember geometry trig, you'll remember a handy mnemonic: SOH CAH TOA. SOH means "sine equals opposite over hypotenuse", and in this case, the opposite side from angle A is the green line h while the hypotenuse is side C. Therefore, we can say that sineA= h/c.
But what about the other triangle we made? We can apply SOH to this triangle too, and we get sinC=h/a.
As you can see, h is in both of these equations, so if we fiddle a bit to get h by itself in both equations (multiplying both sides by c in the first, multiplying both sides by a in the second), we can set the two equal to each other. Now we have c(sinA)= a(sinC). Fiddle around a bit more (and by that I mean divide both sides by ac- a term both sides have) and you're left with the Law of Sines...sort of.

It's almost there, but what about angle B? We can't just leave it all by itself!
Not to worry, we can just make another green perpendicular line and do the same thing, only with different angles.
In this case, SOH for the two triangles are sinA=h/b and sinB=h/a. Do the same fiddling to get h by itself to set the two equations equal to each other and we get b(sinA)=a(sinB). Fiddle again and we end with this lovely bit:
Still not the Law of Sines, but we're close. As you can see, both equations have sinA/a in them. Which means...we can set them equal to each other! Yay! And for added fun, we don't even have to get rid of sinA/a! We can just mash them together to get this:

And there's the Law of Sines. Isn't it lovely?
[4] Area Formulas
How is the “area of an oblique” triangle derived? How does it relate to the area formula that you are familiar with?I'm going to go ahead and answer both of these questions in one chunk. Less reading, how lucky for you!
Below are some examples of an oblique triangle (aka a triangle with all sides not being equal.)

As you can see, we start by doing the same thing we did before- make right triangles with a perpendicular line called h because mathematicians love right triangles more and we already know how to work with them.
If you recall from reading the Law of Sines section above, you'll know that we can get h by itself at some point with any of the angles. you have the option of a(sinB), a(sinC), b(sinA), b(sinC), c(sinA) and c(sinB) depending on which angle you sacrificed to draw h. Why is getting h by itself so important, you might ask? Again, if you remember geometry, you'll know the area of a triangle is usually given as a=1/2(b)(h). Oh look at that, there's an h in that equation that we can conveniently substitute any of the above options into, how fortunate for us!
Let's go with the first option, a(sinC) for simplicity's sake. When we substitute that value into the area equation, we get...
/drumrolls/
...1/2 (b)(a)(sinC)! And that's our area of an oblique triangle equation.
References:
http://www.mathsisfun.com/algebra/trig-sine-law.html
http://www.regentsprep.org/Regents/math/algtrig/ATT12/lawofsines.htm
http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm
Why do we need it?
We need the Law of Sines when we are not sure if a triangle is a right triangle.
How is it derived from what we already know?
Since we don't know if the triangle we're given is a right triangle, we can't use the trig ratios we used in the Unit Circle. However, we can use trig functions. Say we're given the triangle below.

We don't know if it is a right triangle, but that doesn't matter because we can just do this
If you remember geometry trig, you'll remember a handy mnemonic: SOH CAH TOA. SOH means "sine equals opposite over hypotenuse", and in this case, the opposite side from angle A is the green line h while the hypotenuse is side C. Therefore, we can say that sineA= h/c.
But what about the other triangle we made? We can apply SOH to this triangle too, and we get sinC=h/a.
As you can see, h is in both of these equations, so if we fiddle a bit to get h by itself in both equations (multiplying both sides by c in the first, multiplying both sides by a in the second), we can set the two equal to each other. Now we have c(sinA)= a(sinC). Fiddle around a bit more (and by that I mean divide both sides by ac- a term both sides have) and you're left with the Law of Sines...sort of.

It's almost there, but what about angle B? We can't just leave it all by itself!
Not to worry, we can just make another green perpendicular line and do the same thing, only with different angles.
In this case, SOH for the two triangles are sinA=h/b and sinB=h/a. Do the same fiddling to get h by itself to set the two equations equal to each other and we get b(sinA)=a(sinB). Fiddle again and we end with this lovely bit:
Still not the Law of Sines, but we're close. As you can see, both equations have sinA/a in them. Which means...we can set them equal to each other! Yay! And for added fun, we don't even have to get rid of sinA/a! We can just mash them together to get this:

And there's the Law of Sines. Isn't it lovely?
[4] Area Formulas
How is the “area of an oblique” triangle derived? How does it relate to the area formula that you are familiar with?I'm going to go ahead and answer both of these questions in one chunk. Less reading, how lucky for you!
Below are some examples of an oblique triangle (aka a triangle with all sides not being equal.)

As you can see, we start by doing the same thing we did before- make right triangles with a perpendicular line called h because mathematicians love right triangles more and we already know how to work with them.
If you recall from reading the Law of Sines section above, you'll know that we can get h by itself at some point with any of the angles. you have the option of a(sinB), a(sinC), b(sinA), b(sinC), c(sinA) and c(sinB) depending on which angle you sacrificed to draw h. Why is getting h by itself so important, you might ask? Again, if you remember geometry, you'll know the area of a triangle is usually given as a=1/2(b)(h). Oh look at that, there's an h in that equation that we can conveniently substitute any of the above options into, how fortunate for us!
Let's go with the first option, a(sinC) for simplicity's sake. When we substitute that value into the area equation, we get...
/drumrolls/
...1/2 (b)(a)(sinC)! And that's our area of an oblique triangle equation.
References:
http://www.mathsisfun.com/algebra/trig-sine-law.html
http://www.regentsprep.org/Regents/math/algtrig/ATT12/lawofsines.htm
http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm
Thursday, March 6, 2014
WPP#12: Unit O Concept 12: Angles of Elevation and Depression
Create your own Playlist on LessonPaths!
Monday, March 3, 2014
I/D# 2: Unit O Concepts 7-8: Deriving Patterns for the SRTs
Inquiry Activity Summary
1.) 30-60-90 SRT
We start with an equilateral triangle with side lengths 1 and split it in half in a way that bisects an angle and is perpendicular to the side opposite.
Each angle has a value of 60º (so bisecting them would get two 30º angles) and each side has a value of 1 (so making the 'cut' perpendicular to the side opposite would get you two 90º angles and side lengths of 1/2.)
Use the Pythagorean theorem (a^2 + b^2 = c^2) to find the missing leg length. 1/2 (let's say it's a) squared is 1/4, and 1 (let's say it's c) squared is just 1. When you subtract 1/4 from 1 to solve for b you get 3/4, the square root of which is radical 3 over 2.
To get rid of the fractions and make life easier for ourselves we multiply all the terms by 2. This results in the shortest leg equaling 1, the other leg equaling radical 3, and the hypotenuse equaling 2. We now set n equal to 1 (we choose n because it's a variable and we choose 1 because it's in all of the terms) so we can use it for number values other than 1, 2 and radical 3. Therefore, the pattern is n (shortest leg), 2n (hypotenuse- think of it as 2 times 1 and replace the 1 with n), and n radical 3 (other leg- again, think of it as 1 times radical 3 and replace the 1 with n.)
2.) 45-45-90 SRT
We start with a square with side lengths of 1 and split it in half diagonally.
This bisects the corner angles, which have a value of 90º each. 90/2 = 45º.
We know the two legs of the triangle each equal 1, so to find the hypotenuse we use the Pythagorean theorem (a^2 + b^2 = c^2). a and b represent the legs of the triangle, so we set them both equal to 1; 1 squared is just 1, so 1 + 1 = 2. c therefore equals radical 2.
We now set n equal to 1 (we choose n because it's a variable and we choose 1 because it's in all of the terms) so we can use it for number values other than 1 and radical 2. Therefore, the pattern is n (one leg), n (other leg), and n radical 2 (for the hypotenuse- think of it as 1 times radical 2 and replace the 1 with an n.)
Inquiry Activity Reflection
1.) “Something I never noticed before about special right triangles is…” that they were derived from an equilateral triangle and a square.
2.) “Being able to derive these patterns myself aids in my learning because…” I now know how to derive the side lengths myself instead of relying on my subpar memory.
1.) 30-60-90 SRT
We start with an equilateral triangle with side lengths 1 and split it in half in a way that bisects an angle and is perpendicular to the side opposite.
Each angle has a value of 60º (so bisecting them would get two 30º angles) and each side has a value of 1 (so making the 'cut' perpendicular to the side opposite would get you two 90º angles and side lengths of 1/2.)
Use the Pythagorean theorem (a^2 + b^2 = c^2) to find the missing leg length. 1/2 (let's say it's a) squared is 1/4, and 1 (let's say it's c) squared is just 1. When you subtract 1/4 from 1 to solve for b you get 3/4, the square root of which is radical 3 over 2.
To get rid of the fractions and make life easier for ourselves we multiply all the terms by 2. This results in the shortest leg equaling 1, the other leg equaling radical 3, and the hypotenuse equaling 2. We now set n equal to 1 (we choose n because it's a variable and we choose 1 because it's in all of the terms) so we can use it for number values other than 1, 2 and radical 3. Therefore, the pattern is n (shortest leg), 2n (hypotenuse- think of it as 2 times 1 and replace the 1 with n), and n radical 3 (other leg- again, think of it as 1 times radical 3 and replace the 1 with n.)
2.) 45-45-90 SRT
We start with a square with side lengths of 1 and split it in half diagonally.
This bisects the corner angles, which have a value of 90º each. 90/2 = 45º.
We know the two legs of the triangle each equal 1, so to find the hypotenuse we use the Pythagorean theorem (a^2 + b^2 = c^2). a and b represent the legs of the triangle, so we set them both equal to 1; 1 squared is just 1, so 1 + 1 = 2. c therefore equals radical 2.
We now set n equal to 1 (we choose n because it's a variable and we choose 1 because it's in all of the terms) so we can use it for number values other than 1 and radical 2. Therefore, the pattern is n (one leg), n (other leg), and n radical 2 (for the hypotenuse- think of it as 1 times radical 2 and replace the 1 with an n.)
Inquiry Activity Reflection
1.) “Something I never noticed before about special right triangles is…” that they were derived from an equilateral triangle and a square.
2.) “Being able to derive these patterns myself aids in my learning because…” I now know how to derive the side lengths myself instead of relying on my subpar memory.
Subscribe to:
Comments (Atom)










